Resampling Algorithms

15 September 2017

Given a set of normalized weights \((w_n)_{n = 1}^N\), the goal of a resampling algorithm is to return a set of indices \((i_n)_{n = 1}^N\) such that for \(k = 1, \dotsc, N\): \begin{align} \E\left[\frac{1}{N} \sum_{n = 1}^N \mathbb 1(i_n = k)\right] = w_k. \end{align}

We consider the multinomial, stratified, and systematic resampling algorithms which can be implemented in Python as follows:

import numpy as np

def resample(weights, algorithm):
    num_weights = len(weights)
    if algorithm == 'multinomial':
        uniforms = np.random.rand(num_weights)
    elif algorithm == 'stratified':
        uniforms = np.random.rand(num_weights) / num_weights + np.arange(num_weights) / num_weights
    elif algorithm == 'systematic':
        uniforms = np.random.rand() / num_weights + np.arange(num_weights) / num_weights
    else:
        raise NotImplementedError()

    return np.digitize(uniforms, bins=np.cumsum(weights))

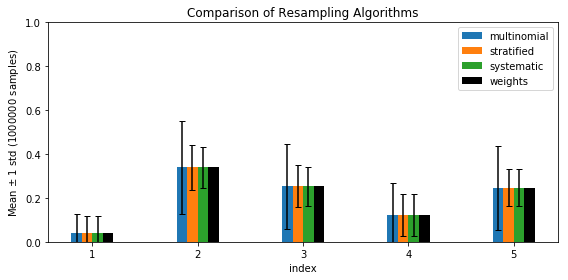
This function returns a set of indices \((i_n)_{n = 1}^N\) for which the above condition holds. However, the variance \(\Var\left[\frac{1}{N} \sum_{n = 1}^N \mathbb 1(i_n = k)\right]\) can be different. In the figure below, we plot empirical mean and standard deviation of \(\frac{1}{N} \sum_{n = 1}^N \mathbb 1(i_n = k)\) using \(1000000\) samples where \(x\) axis iterates over \(k = 1, \dotsc, K\):